7.次の計算をしなさい。【小4】
① 18.3÷7 の計算をしなさい。
答えは四捨五入して小数第1位までの概数(がいすう)で求めなさい。
② 0÷4=
③ 1÷0=

①18.3÷7=2.61… 答え:2.6
②0÷4=0
③1÷0.01=100
1÷0.0001=10000
1÷0.00000…1=100000…0
答え:無限大
8.分数と小数はどちらが多いですか。【小5】
2の倍数と3の倍数はどちらが多いですか。
【ヒント】「多い」とはどういうことでしょう。

分数も小数も無限にありますから、どちらが多いかという比較はできません。「あるものよりあるものの方が多い」というのは、個数が有限でないと比較できないのです。
2の倍数も3の倍数も同様に無限にあるので、比較することはできません。
【参考】
興味のある人は、次のことばをネットで検索してみて下さい。
「集合の濃度」
9.円周率は3より大きいことを示しなさい。【小5】
【ヒント】「円周率」とは 何÷何 だったか。 円周率とは、「円周は直径の何倍か」でした。

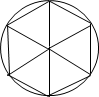
円に内接する正六角形をかいて、右の図のように6つに分割すると、
内部に正三角形が6つできます。
その周は半径の6倍です。ということは直径の3倍になります。
それぞれの三角形の辺と円周の一部である弧を比べると、
2点を結んだ線分が最短ですから、円周は直径の3倍よりは長いことになります。
円に内接する正六角形をかいて、右の図のように6つに分割すると、
内部に正三角形が6つできます。
その周は半径の6倍です。ということは直径の3倍になります。
それぞれの三角形の辺と円周の一部である弧を比べると、
2点を結んだ線分が最短ですから、円周は直径の3倍よりは長いことになります。
10.行きは時速5km,帰りは時速6kmで歩いた。往復の平均の速さを求めなさい。【小6】

片道の道のりを1とすると、行きにかかった時間は
時間=道のり÷速さ=\(\frac{1}{5}\)
帰りにかかった時間は
時間=道のり÷速さ=\(\frac{1}{6}\)
往復にかかった時間は
\(\frac{1}{5}\)+\(\frac{1}{6}\)=\(\frac{11}{30}\)
また往復の道のりは2だから、往復の平均の速さは
速さ=道のり÷時間=2÷\(\frac{11}{30}\)
よって、求める平均の速さは時速 5\(\frac{5}{11}\) km