小学６年で次の問題が５分以内に解けたら、難関中学に合格できます。

3.底面の半径が56cmで、母線の長さが2.5cmの円錐の表面積を求めなさい。

円錐の表面積は、底面積と側面積の和になります。
底面積＝半径×半径×3.14
側面積は、母線を半径とする円の一部である扇形ですから、
側面積＝母線×母線×3.14×（半径÷母線）
＝母線×半径×3.14
この２つを足すと、
表面積＝半径×半径×3.14＋母線×半径×3.14
＝（半径＋母線）×半径×3.14
＝ \(8\frac{13}{18}cm^2\) でも、次の問題が解けないと、AI時代に役に立つ人財にはなれません。

---

でも、次の問題が解けないと、AI時代に役に立つ人財にはなれません。

---

4.次の形の面積を求めなさい。

面積とは広さのことですが、算数ではただ広いというだけでなくて、
どのくらい広いかを数字で表そうとします。
そのためにははかりと単位が必要になります。
広さの単位となるのは、縦１、横１の正方形です。
それが何個分あるかで広さを表すのです。
そこで、縦・横ともに $\frac{1}{4}$ の幅で線を引くと、

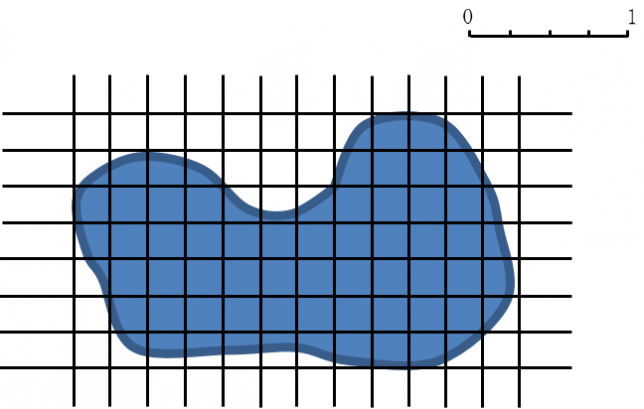
できた正方形の数を数えると、
①欠けていない正方形が　39個
②欠けている正方形が　　34個
です。さらに、
欠けていない正方形の面積は $\frac{1}{16}$
欠けている正方形の面積は半分にして $\frac{1}{32}$
とすると、求める面積は
$\frac{1}{16}×39 + \frac{1}{32}×34 ＝ 3.5$
となります。